The foundations of the backpropagation method for learning in neural networks were laid by [RHW86].
Artificial neural networks consist of many simple processing devices
(called processing elements or neurons) grouped in layers. Each layer
is identified by the index ![]() . The layers and L are
called the ``input layer'' and ``output layer'', all other layers are
called ``hidden layers''. The processing elements are interconnected as
follows: Communication between processing elements is only allowed for
processing elements of neighbouring layers. Neurons within a layer
cannot communicate. Each neuron has a certain activation level a.
The network processes data by the exchange of activation levels
between connected neurons (see figure 1):
. The layers and L are
called the ``input layer'' and ``output layer'', all other layers are
called ``hidden layers''. The processing elements are interconnected as
follows: Communication between processing elements is only allowed for
processing elements of neighbouring layers. Neurons within a layer
cannot communicate. Each neuron has a certain activation level a.
The network processes data by the exchange of activation levels
between connected neurons (see figure 1):
xi(l) = g(ai(l))
whereai(l) = f(ui(l))
whereThe net input ui(l) of neuron i in layer l is calculated as
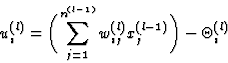
The calculation of the network status starts at the input layer and ends at the output layer. The input vector I initializes the activation levels of the neurons in the input layer:
![]()
The simulation can be divided into two main phases during network training: A randomly selected input/output pair is presented to the input layer of the network. The activation is then propagated to the hidden layers and finally to the output layer of the network.
In the next step the actual output vector is compared with the desired result. Error values are assigned to each neuron in the output layer. The error values are propagated back from the output layer to the hidden layers. The weights are changed so that there is a lower error for a new presentation of the same pattern. The so called ``generalized delta rule'' is used as learning procedure in multi layered perceptron networks.
The weight change in layer l at time v is calculated by
![]()
![]()
The formula can be explained as follows: When the output xk(l) of the
neuron i in layer l is too small, ![]() has a
negative value. Hence the output of the neuron can be raised by
increasing the net input uk(l) by the following change of the
weight values:
has a
negative value. Hence the output of the neuron can be raised by
increasing the net input uk(l) by the following change of the
weight values:
if xi(l-1) > 0, then increase wki(l)
if xi(l-1) < 0, then decrease wki(l)
The rule applies vice versa for a neuron with an output value that is too high (see figure 2).
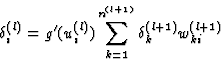
Finally the weights of layer l are adjusted by
![]()
| © 1997 Gottfried Rudorfer, © 1994 ACM APL Quote Quad, 1515 Broadway, New York, N.Y. 10036, Abteilung für Angewandte Informatik, Wirtschaftsuniversität Wien, 3/23/1998 |